Roadmap to Becoming a Data Scientist, Part 1: Maths
Identifying fundamental math skills for aspiring data scientists
Introduction
Data science is undoubtedly one of the most fascinating fields today. Following significant breakthroughs in machine learning about a decade ago, data science has surged in popularity within the tech community. Each year, we witness increasingly powerful tools that once seemed unimaginable. Innovations such as the Transformer architecture, ChatGPT, the Retrieval-Augmented Generation (RAG) framework, and state-of-the-art computer vision models — including GANs — have had a profound impact on our world.
However, with the abundance of tools and the ongoing hype surrounding AI, it can be overwhelming — especially for beginners — to determine which skills to prioritize when aiming for a career in data science. Moreover, this field is highly demanding, requiring substantial dedication and perseverance.
In this article, I aim to present a detailed roadmap outlining the key areas in math to focus on when starting your journey in data science.
This article will focus solely on the math skills necessary to start a career in Data Science. Whether pursuing this path is a worthwhile choice based on your background and other factors will be discussed in a separate article.
Data Science — view from outside
In many ways, data science stands out as a unique domain, as it demands a diverse set of skills spanning multiple disciplines. In my view, a Venn diagram serves as an excellent visual representation of what data science truly encompasses:
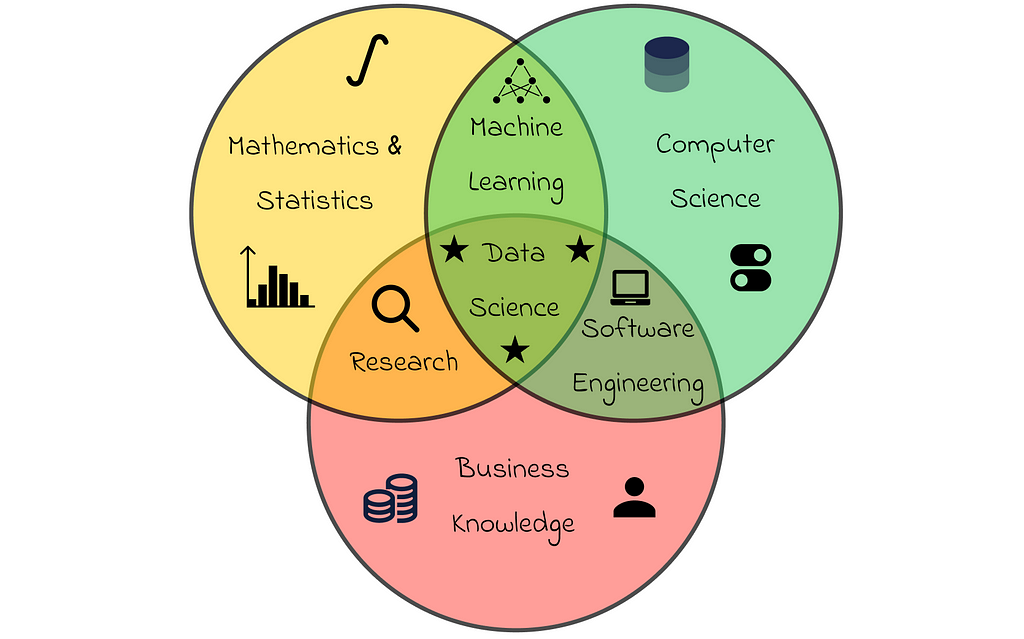
As we can see, data science lies at the intersection of three key areas: mathematics, computer science, and business expertise. While all three components are essential, I recommend that beginners concentrate primarily on the first two.
The reason for this recommendation is that a solid foundation in mathematics and computer science is essential for any Data Scientist role. Meanwhile, data science is applied across a wide range of domains, including banking, e-commerce, supply chain, healthcare, self-driving cars, and more. As a result, the specific business domain you work in may change frequently throughout your career.
While it is still valuable to invest effort in understanding a particular business domain, this factor is often variable. Therefore, I strongly recommend prioritizing mathematics and computer science as core skills. These areas will be the primary focus of this article series.
Motivation
Mathematics forms the foundational building block of all machine learning algorithms. Without a solid understanding of math, it is impossible to grasp how these algorithms function.
Can you still train and use machine learning models without fully understanding how they work? Yes, you can. There are numerous excellent tools and libraries — such as Scikit-Learn, TensorFlow, PyTorch, and Gym — that enable you to train complex models with just a few lines of code. So, why should you even bother learning math in such a case?
Understanding how algorithms work under the hood helps you make informed decisions when selecting the most appropriate algorithm for a given task. It also enables you to recognize its scope, debug and optimize it more easily, and choose better parameters. Additionally, with this valuable knowledge, you can modify the original algorithm to better suit your specific needs.

Furthermore, many algorithms are built upon one another, so grasping the fundamentals of basic algorithms will make it easier to understand more advanced ones.
Finally, in a data science career, it is often necessary to review recent scientific publications. As a general rule, machine learning articles and papers frequently contain numerous mathematical notations and formulas. To fully understand their context, a strong foundation in mathematics is essential.
Given the points I have outlined, I hope the importance of learning math is now clear. Next, let us discuss the specific mathematical skills you need to develop as an aspiring Data Scientist.
# 01. Calculus
Calculus is a vast field, encompassing a abundance of beautiful equations, theorems, and concepts. Without this knowledge, understanding the inner workings of basic machine learning algorithms would be nearly impossible. The good news is that Data Scientists do not need to know all of it, as only a few key concepts are used in the most important algorithms. The diagram below illustrates the essential knowledge to focus on initially:
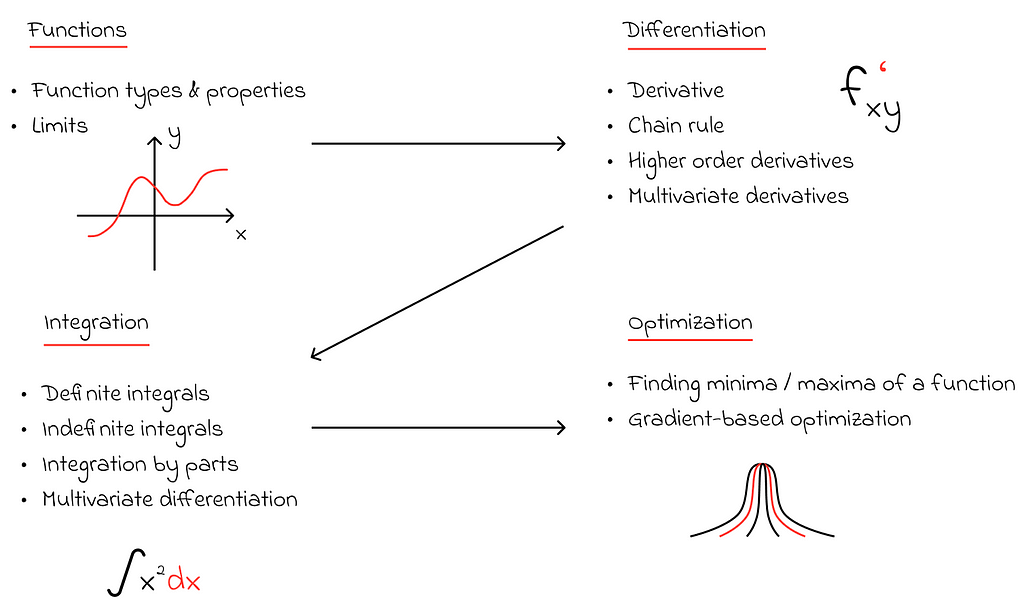
Many machine learning algorithms are based on optimization problems, where the goal is to find the minimum of a function, typically through the calculation of derivatives.
While integrals are not as commonly used in machine learning, they remain very useful in statistics and probability theory — another important area we will focus on later in this article. In simple terms, integrals are the inverse operation of derivatives. As it turns out, integrals and derivatives are closely linked, and many theorems rely on both to prove key concepts.
Reaching a point where you understand how derivatives are used will help you grasp the Stochastic Gradient Descent (SGD) algorithm, a fundamental method employed by most machine learning algorithms.
While algorithms are constantly evolving and many scientific papers rely on advanced mathematical concepts, they become much easier to understand once you have a solid foundation in the basics of calculus.
# 02. Linear algebra
Linear algebra is another key area of mathematics that focuses on vectors, vector spaces, and linear transformations.
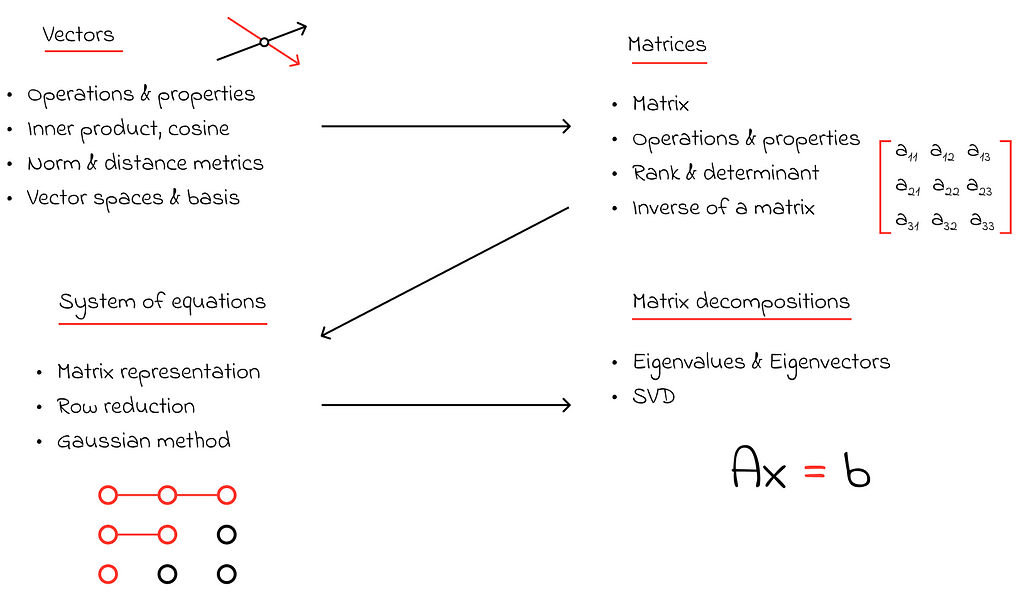
In data science, data can be represented in various formats, but ultimately, it is converted into vectors of numbers that are fed into a predictive model. Vectors are also used to compare similarities between objects, estimate correlations between variables, perform feature engineering, update model weights, or encode the semantic meanings of words. Given their broad range of applications, it is crucial to study vectors early on.
The next important topic is matrices, which can be viewed as a collection of several vectors stacked together into a table. Matrices are used to represent tabular data or graphs. They are also widely used in neural networks, where a layer of the network can be represented as a matrix. This matrix representation enables faster calculations, as many mathematical approaches are optimized to work more efficiently with matrices than if the same calculations were done without them.
Another important application of matrices is in solving systems of linear equations. Each such system can be represented as a matrix equation: Ax = b. Given this, there are several methods to solve the equation, based on matrix properties such as multiplication, finding the determinant, or calculating the inverse matrix.
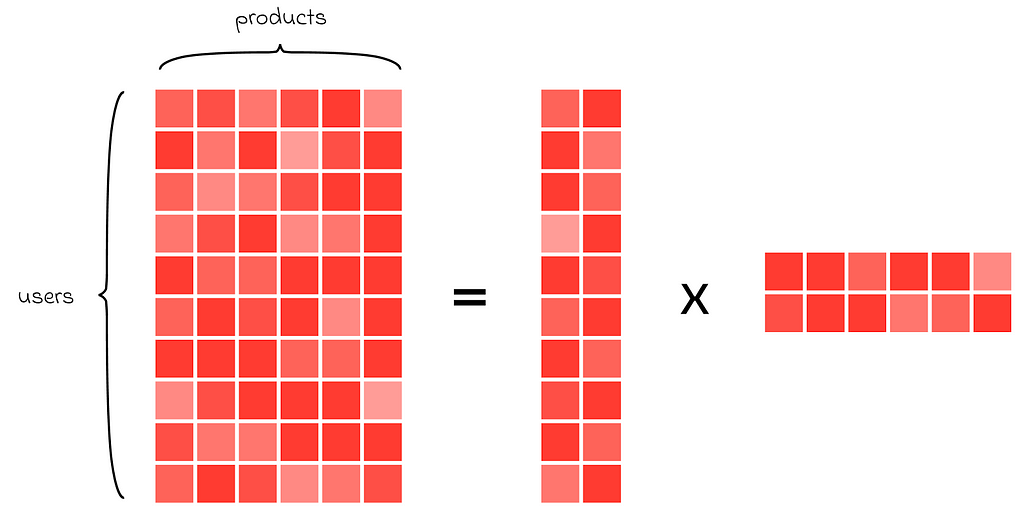
Finally, matrices can not only represent tabular data but also be used to compress it through matrix decomposition. This process involves representing the original matrix as the product of several smaller matrices. This method is particularly popular in recommender systems, where relationships between a large database of users and products can be stored as a combination of smaller, more efficient matrices.
# 03. Statistics
In data science, Exploratory Data Analysis (EDA) is a crucial part of data analysis, involving the exploration of data, detection of anomalies, formulation of assumptions about relationships between variables, and studying their impact on the predictive variable. All of this requires a strong foundation in statistics.
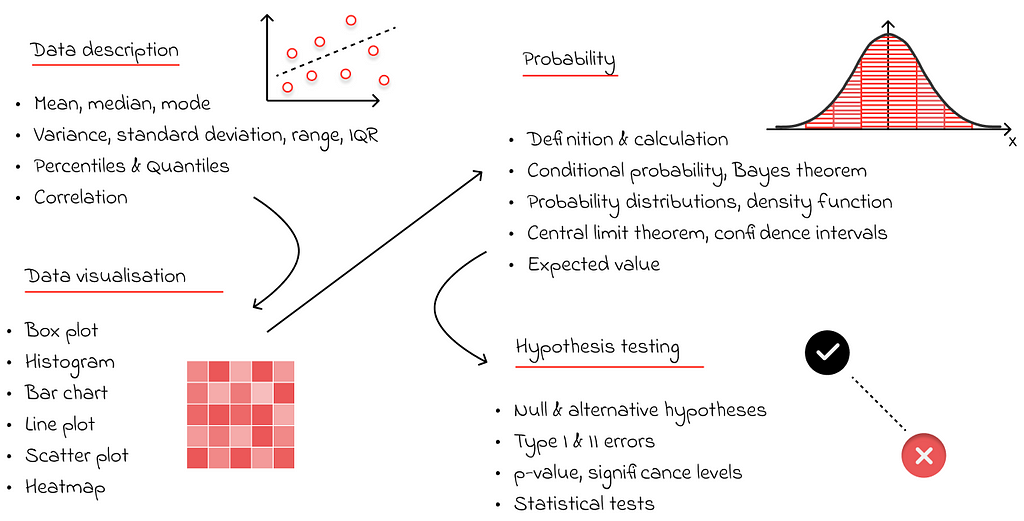
To effectively describe data, one must study basic descriptive statistics and methods for visually representing data. This is one of the simplest yet most important areas of mathematics.
Probability theory is another fundamental building block that appears in many areas of computer science. In the context of machine learning, there are numerous metrics used to evaluate the quality of an algorithm, many of which are based on probability definitions, such as precision, recall, and ROC AUC. There are even probabilistic models, such as the Naive Bayes algorithm, which is used for classification tasks.
Furthermore, classical probability theory includes various types of data distributions, with the normal distribution being particularly important. Its significance cannot be overstated, as it can be applied to describe a wide range of real-world processes. Finally, the introduction of the central limit theorem and confidence intervals provides a foundation for understanding the next major topic in statistics: hypothesis testing.
A/B tests, which are based on hypothesis testing, are another important topic in data science. The goal of A/B testing is to determine whether there is a significant difference in a given metric between two groups of objects that were initially split based on a specific criterion.
For example, imagine a supermarket conducting an experiment to determine whether sending SMS messages to its customers will increase the total revenue. To start, the entire customer database is taken and randomly divided into two groups, ensuring there is no existing bias. These groups are labeled A and B. Then, the marketing campaign begins, and the supermarket sends SMS messages to all customers in group A, while those in group B receive no communication.
After an initially defined period of time, the revenue is calculated for both groups. If there is a significant difference in revenue between the two groups, considering the initial settings, then we can conclude that sending SMS messages has an impact on the generated revenue.
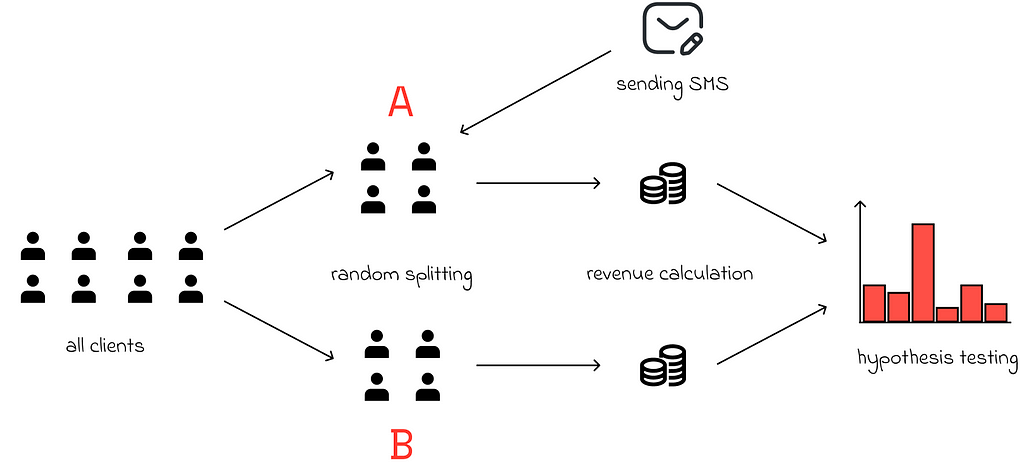
The provided example is quite simplified, as the actual science behind A/B testing is much more complex. Nevertheless, hypothesis testing is a fundamental component of A/B tests, as it explains the underlying logic and offers various methods for conducting A/B tests in different scenarios.
# 04. Discrete mathematics
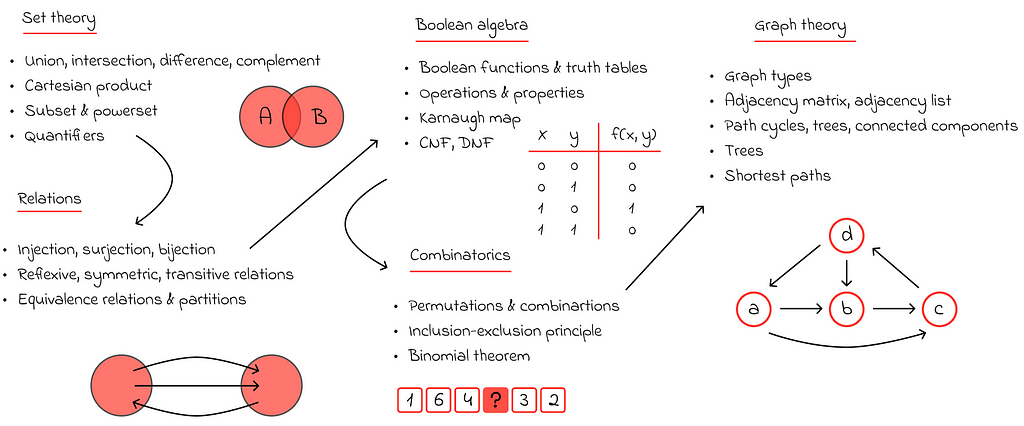
In my personal experience, discrete mathematics is the easiest branch of mathematics to study, compared to the previous ones. As the name suggests, discrete mathematics studies mathematical structures where the variables are discrete (not continuous).
Many books and courses introduce discrete mathematics by starting with set theory, which makes sense since sets are used almost everywhere to formally define other structures, express complex mathematical constraints concisely, and formally prove various statements and theorems. Additionally, the notation used in set theory is widely adopted in machine learning papers, as seen in the example below:

The next important branch is relations and functions, which study the relationships between elements of sets. While it is rare to encounter a direct application of relation theory in real-world data science problems, its knowledge remains valuable. This is because many proofs in other domains, especially in graph theory, can be simplified by applying concepts and properties of relations.
Boolean algebra, which deals with boolean functions that operate on binary variables, is another key area. The interesting thing is that it would be impossible to imagine modern computers without boolean algebra. In fact, at the low level, computers only operate with 0s and 1s, and all computations are carried out based on the principles of boolean algebra.
Knowledge of boolean algebra helps in understanding logical conditions and operators in code, filtering data in SQL and other languages using logical operators, optimizing queries, and performing data processing.
Combinatorics is a branch of mathematics focused on counting and arranging objects within finite data structures. This knowledge is useful for estimating how many samples or trials are needed to conduct an experiment, optimizing sampling techniques, dividing objects into subsets, or computing the number of possible paths in a graph.
While tables remain the most popular format for data representation, they cannot directly store the relationships between objects. This is where graphs come into play. A graph is a data structure consisting of vertices that represent objects and edges that store the relationships between them. Depending on the type of edge, it can either indicate the presence or absence of a relationship between a pair of vertices or store a weight that signifies the strength or weakness of the relationship.
This seemingly simple structure is supported by an entire field of study called graph theory. Graph theory explores various types of graphs and their properties, such as grouping vertices into components based on their connectivity with other vertices, or finding the shortest path between two vertices.
An obvious application of graphs is the analysis of social networks. A network of people can be viewed as a graph, where each vertex represents a person, and the edges connecting it lead to other people that the person knows. While this is the most commonly used example when discussing graphs, their application scope is vast and extends beyond social networks to any domain where relationships between objects exist. In particular, graph theory is widely used in logistics optimization problems.
Should I study proofs of theorems?
This is a common question that arises among math learners. All four of the math blocks we have discussed contain numerous statements and theorems that have been rigorously proven. The challenge is that fully understanding the logic behind a proof often takes a considerable amount of time. So, is it really worth investing time in proof analysis?
In my personal experience, analyzing and deeply engaging with proofs played an important role during my university studies. On one hand, it is clear that, after graduation, I do not actually remember most of those proofs — something that is completely normal, as our brains tend to forget information we do not frequently revisit.
On the other hand, being able to understand the reasoning behind almost every math theorem I encountered in the past helped me become less intimidated when facing unfamiliar statements in new machine learning papers. It also sparked a desire to explore why those statements are true. Additionally, this approach promotes abstract thinking, which is important for success as a Data Scientist.
In the end, my answer would be yes — you should go through the proofs of mathematical theorems you encounter when studying basic math to become a Data Scientist.
In other cases:
- If you do not have much time to study, focus on the most important proofs or just try to understand the deep meaning behind the theorem statements.
- If you do not enjoy studying proofs at all, ask yourself whether you truly enjoy math and if you are certain about pursuing a career in data science.
Conclusion
In this roadmap, we have explored the four most important branches of mathematics to study for data science. While the list of terms and concepts presented in the text and diagrams could certainly be expanded, I have focused on the most essential ones.
What is important to recognize is that even if you have a strong grasp of the core math domains, there will still be moments when you encounter new concepts. This is perfectly normal, as machine learning is constantly evolving, and it is impossible to cover everything in detail. However, having a solid understanding of the foundational math concepts will allow you to grasp new methods and algorithms more quickly, and this is what truly matters in today’s data science market.
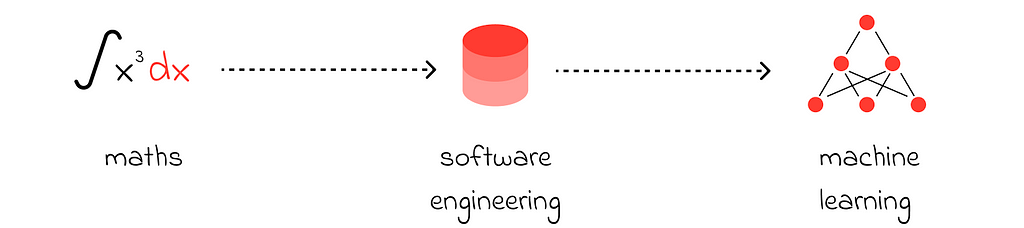
In the next articles of this series, we will focus on the software engineering and machine learning skills necessary for data science.
Connect with me: ✍️
Resources
All images are by the author unless noted otherwise.
Roadmap to Becoming a Data Scientist, Part 1: Maths was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Datascience in Towards Data Science on Medium https://ift.tt/DIacqlK
via IFTTT




