Datascience in Towards Data Science on Medium,

Writing LLMs in Rust: Looking for an Efficient Matrix Multiplication

11/14/2024 Jesus Santana

Starting from Karpathy llm.c, I wonder myself “Could I write this in Rust?” Here are the lessons I learned and how I am writing llm.rust. In this first article, let’s tackle the matrix multiplication problem.

Matrix multiplication may be the most important operation in Machine Learning. I still remember when I was an engineering student, and in one of the first linear algebra lessons, the teacher started to explain matrices, eigenvectors, and basis and orthonormal basis. I was very confused, my head took a little while to start understanding why we were bothering so much about matrices and basis sets, and what a good basis implies for our world. From there, I always found linear algebra so fascinating, and, from a pure computer science point of view, how amazing all those algorithms that try to be more and more efficient in handling matrices.

In particular, we know that the matrix-vector product is pretty simple, but things are getting more and more complicated when we have matrices-matrices or tensors-tensors products. From here, many methodologies have been implemented to optimize the matrix multiplication. For example, a long time ago I posted about DeepMind matrix multiplication methodology and Strassen algorithm. This problem still fascinates me a lot, and I was so amused and happy to see llm.c by Karpathy.

As matter of fact, the core part of the attention algorithm — well of all the ML algorithms — is, of course, the matrix multiplication. For my project, I started from one of the very early commits of Karpathy’s repository (here is the matrix multiplication). Most of the time is spent on this function, thus optimize this calculation definitely would help us in lowering the training cost of LLM. Eq.1 shows the formula we are dealing with in LLMs:

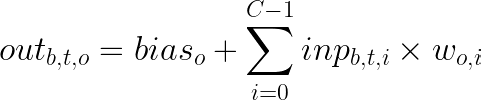
We have an output tensor out, whose dimensions are B, the batch index, defined from 0 to B-1, the time step t, defined from 0 to T-1, and the output channel o, from 0 to OC-1. The output is defined as the sum of the bias, and the tensor product between the input embeddings and the model’s weights w. In the context of attention mechanism, the matrix multiplication comes into play in the Q, K and V calculation. Given an embedding input X, there is a linear transformation to project the embedding into query Q, key K and value V vectors:

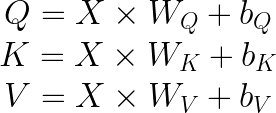
Where, W represents the query (underscore Q), key (underscore K) and value (underscore V) weights, while b is the associated bias.

Likewise, the matrix multiplication is present on the back-propagation step, where we’re running the backward matrix multiplication. Backward matrix multiplication computes the gradients with respect to the inputs, weights and biases, returning the gradient of the loss with respect to the outputs.

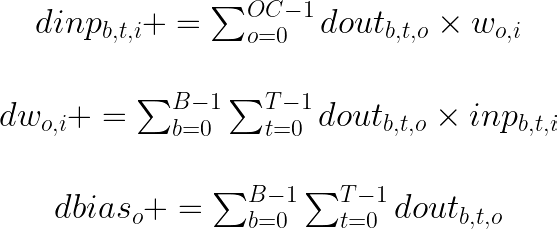
Eq. 3 summarizes the backward matrix multiplication. dinp is the gradient of the loss with respect to the input embeddings, inp in eq. 1. This equation updates dinp by accumulating the product of the gradients from the outputs and their corresponding weights. Then, we compute the gradient of the loss with respect to the weights, accumulating the product of the gradients from the output and the corresponding inputs. Finally, if any bias is present, we compute the gradient of the loss with respect to the bias, summing up the gradients from the outputs over all the batches B, and times steps T for each output channel OC.

Given this amazing piece of code, I wondered if I could do something something similar in Rust, to help me learning more and more this programming language, and try to achieve some sort of training on my MacBook. The code that’s referring to this article can be found here. Be aware, the code is work in progress, so it may change day-by-day.

This article doesn’t want to compare implementations speed, as this depends on several variables (we could use GPUs, data sharding, vectorization, quantization, distillation). What I want to do is to find the best method to be used in my LLM implementation in Rust, and try to run my code for training an LLM on my MacBook M2.

TLDR: my choice for Rust — skipping the code details

If you’re in a rush, here are my choices for the best implementation in Rust, to run the training of a GPT-2 like LLM on a MacBook M2 Pro.

Tab.1 compares the average performance time, in seconds, between C, implemented with OpenMP running on 8 threads, C OpenMp, a base implementation in Rust, Rust base, Rust implementation using Rayon, Rust Rayon, and Blas implementation for Rust, Rust Blas. The input dimensions were B = 64, T = 1024, C = 768, OC = 768, corresponding to an input and output tensor of size 50'331'648 elements.

Overall, Blas, as expected, attains an average of 0.05 s to perform forward matrix multiplication. Likewise, the backward matrix multiplication, performs at best with Blas for Rust, with 0.19 s.

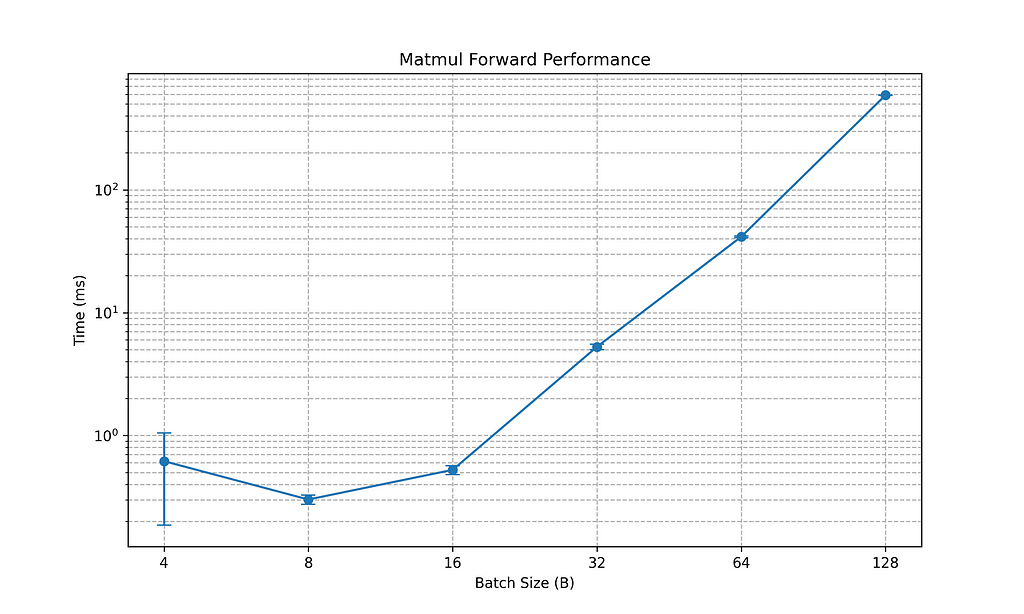
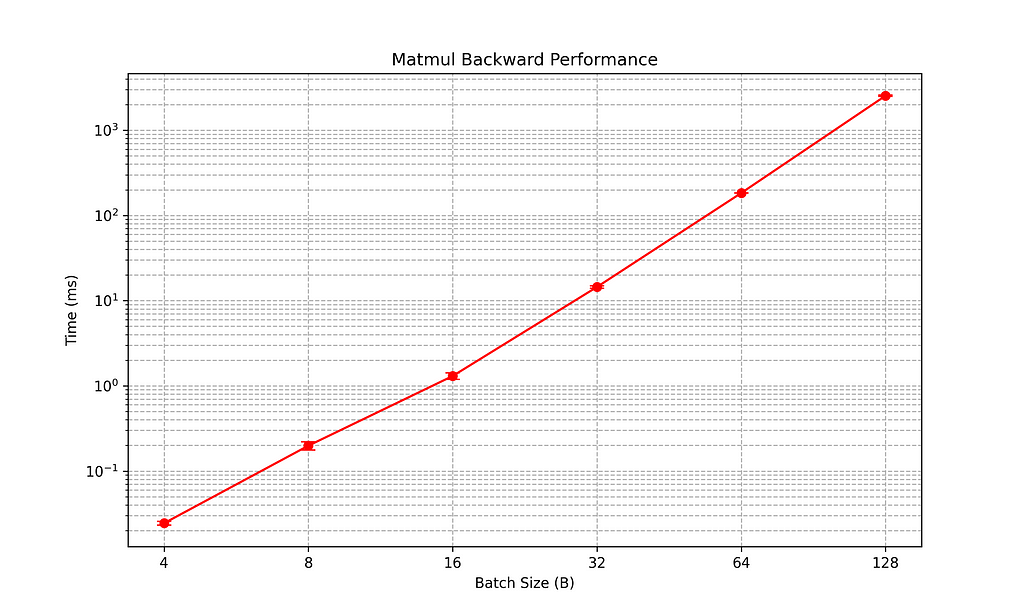
I also tried to push these two calculations to the limits, modifying the batch size from 4 to 128, likewise increasing the time steps from 64 to 2048, and the channel and output channel from 48 to 1536. This means passing from an input and output tensor with 12'288 elements, to 402'653'184 elements. Fig. 1 and 2 represent matmul forward and backward performance for those input values, in a logarithmic scale. For the matmul forward operation, we pass from an average of a microsecond to a max of 0.58 +/- 0.01 s. Similarly, for the backward pass, we range from a microsecond on average to 2.54 +/- 0.05 s. The conclusion here is that Blas is highly optimized to handle very large matrices. Indeed, at a very small scale, B = 4, there is a high variance in the range, passing from 1.20 ms to 0.4 ms.

Naive matrix multiplication in C

I know many people may have an allergy to C and C++, but bear with me, in this case, we’re simplifying a lot of the problem and trying to implement the matrix multiplication using OpenMP — remember the implementation follows eq. 1, and here is the C code

void matmul_forward(float* out,
                    float* inp, 
                    float* weight, 
                    float* bias,
                    int B, int T, int C, int OC) {
    #pragma omp parallel for collapse(2)
    for (int b = 0; b < B; b++) {
        for (int t = 0; t < T; t++) {
            float* out_bt = out + b * T * OC + t * OC;
            float* inp_bt = inp + b * T * C + t * C;
            for (int o = 0; o < OC; o++) {
                float val = (bias != NULL) ? bias[o] : 0.0f;
                float* wrow = weight + o * C;
                for (int i = 0; i < C; i++) {
                    val += inp_bt[i] * wrow[i];
                }
                out_bt[o] = val;
            }
        }
    }
}

Let’s see what’s happening in this code:

• The starting point is the call of the openMP parallelism: #pragma omp parallel for collapse(2) The omp parallel for is a directive, it combines omp parallel and omp for directives. It defines a region that has a parallel for and has to run in parallel. The collapse(2) instructs the compiler to collapse some nested loops into a single large iteration. Usually, collapse creates a single loop that has at least two orders of magnitude more iterations than the original nested loop.
• Then, we do something “weird”, like float* out_bt = out + b*T*OC + t*OC; This is pointer arithmetic in C, namely, we’re calculating the correct index to access elements. Here we’re computing the starting point for the current batch and time step so that all the following indexes are relative to this position. Moreover, this allows us to vectorize the multi-dimensional input, so we’re flattening a multi-dim input into a one-dimensional array, to improve performance. For example, here float* out_bt = out + b*T*OC + t*OC we’re working with the tensor out. This tensor has dimensions B x T x OC. The offset calculation does the following: 1) moves to batch b with b*T*OC and 2) moves to time-step t within batch b with t*OC.
• To further appreciate the pointer arithmetic consider this case: B = 2, T = 3, C = 4, OC = 5. To access the input data inp for batch 1, time step 2, input channel 3 we can calculate: 1) the batch offset b*T*C = 1*3*4 = 12; 2) the time-step offset t*C = 2*4 = 8; 3) the total offset 12+8 = 20. In the final loop, we’re iterating the index i, for an input i=3 we’ll have a total offset equal to 23. Thus input[23] corresponds to the input input[1][2][3].

A little caveat, if you’re running on a MacOS you may need to install llvm (so brew install llvm ) and export the paths. In my case, here is how I’ve compiled and run the code:

#!/bin/bash

export OMP_NUM_THREADS=4
export LDFLAGS="-L/opt/homebrew/opt/llvm/lib"
export CPPFLAGS="-I/opt/homebrew/opt/llvm/include"

/opt/homebrew/opt/llvm/bin/clang -O2 -fopenmp $LDFLAGS $CPPFLAGS  -o matmul_example matmul_example.c

echo "Run"
./matmul_example 64 1024 768 768

where matmul_example.c is the name of the C code.

A naive approach in Rust

The source code (and the cargo build) for the naive approach in Rust can be found here

Let’s have a look at the main function:

fn matmul_forward_standard(
    out: &mut [f32],
    inp: &[f32],
    weight: &[f32],
    bias: Option<&[f32]>,
    b: usize,
    t: usize,
    c: usize,
    oc: usize,
) {

    for bb in 0..b {
        for tt in 0..t {
            let out_offset = (bb * t + tt) * oc;
            let inp_offset = (bb * t + tt) * c;
            let inp_bt = &inp[inp_offset..inp_offset + c];

            for oo in 0..oc {
                let mut val = if let Some(bias_vec) = bias {
                    bias_vec[oo]
                } else {
                    0.0
                };
                let weight_offset = oo * c;
                let w_row = &weight[weight_offset..weight_offset + c];

                for i in 0..c {
                    val += inp_bt[i] * w_row[i];
                }
                out[out_offset + oo] = val;
            }
        }
    }
}

We can see a lot of similarities with C. The pointer arithmetic still holds, and, in Rust, representing multi-dimensional arrays as one-dimensional allows to leverage of contiguous memory storage. This approach, significantly enhances the performance, due to cache locality and a reduced calculation overhead. Again, the input array has size [B][T][C]. The flattening operation occurs with offsets, like inp_offset = (bb * t + tt) * oc:

• bb*t moves the index to the batch, skipping over t timesteps per batch;
• +tt moves to the correct time step within the batch
• *c adjusts for the number of channels per time step

Then we proceed with a slicing, namely inp_bt = &inp[inp_offset..inp_offset + c];, so we are performing sequential access within slices, to improve the performance with the spatial locality.

There’s nothing else weird in this code, we can recognize some common Rust particularities, such as the ownership, borrowing and mutability. In the function, we have:

• immutable references with &f[32], so the input arrays are not modified
• mutable references with &mut [f32], for the output tensor
• option handling, we may not have bias so this is defined as Option<&f[32]>. In the final step of the function, we’re considering it through Some(bias_vec)

Let’s make things a bit better: Rayon

The second approach is made with Rayon. Rayon is a Rust library that allows data-parallelism, that converts sequential computations, like in our case, to parallel ones. We can have high-level parallel constructs, that make use of Rayon’s ParallelIterator and par_sort, or custom constructs, like join, scope and ThreadPoolBuilder.

The function is defined as

fn matmul_forward_rayon(
    out: &mut [f32],
    inp: &[f32],
    weight: &[f32],
    bias: Option<&[f32]>,
    B: usize,
    T: usize,
    C: usize,
    OC: usize,
) {
    out.par_chunks_mut(T * OC)
        .zip(inp.par_chunks(T * C))
        .for_each(|(out_b, inp_b)| {
            for time_idx in 0..T {
                let inp_bt = &inp_b[time_idx * C..(time_idx + 1) * C];
                let out_bt = &mut out_b[time_idx * OC..(time_idx + 1) * OC];

                for o in 0..OC {
                    let mut val = bias.map_or(0.0, |b| b[o]);
                    let w_row = &weight[o * C..(o + 1) * C];
                    for i in 0..C {
                        val += inp_bt[i] * w_row[i];
                    }
                    out_bt[o] = val;
                }
            }
        });
}

We start by creating two parallel iterators: out.par_chunks_mut and inp.par_chunks. The former creates chunks from out array, that have at most T*OC elements at a time, the second does the same for inp array with T*C elements. The zip combines the two iterators into a single iterator pair so that each chunk of out has its corresponding inp chunk ( for_each(|(out_b, inp_b)| {} ). Suppose to have B=2, T=3, C=4, and OC=5, it follows that inp will have 24 elements, has its shape is [2][3][4], and out will have 30 elements, [2][3][5]. The chunk works in this way:

• on the output T*OC will give 3*5=15 elements, so initially all the slices from element 0 to 14 ( out[0]), then another batch with elements from 15 to 29 ( out[1])
• on the input T*C will have 3*4=12 elements, so an initial batch with elements from 0 to 11 , and then a second batch with elements from 12 to 23 :

inp (flattened):

Batch 0:
[ inp[0][0][0], inp[0][0][1], ..., inp[0][0][3],
  inp[0][1][0], ..., inp[0][1][3],
  inp[0][2][0], ..., inp[0][2][3] ]  // Total 12 elements

Batch 1:
[ inp[1][0][0], ..., inp[1][0][3],
  inp[1][1][0], ..., inp[1][1][3],
  inp[1][2][0], ..., inp[1][2][3] ]  // Total 12 elements



Similarly for out:

out (flattened):

Batch 0:
[ out[0][0][0], ..., out[0][0][4],
  out[0][1][0], ..., out[0][1][4],
  out[0][2][0], ..., out[0][2][4] ]  // Total 15 elements

Batch 1:
[ out[1][0][0], ..., out[1][0][4],
  out[1][1][0], ..., out[1][1][4],
  out[1][2][0], ..., out[1][2][4] ]  // Total 15 elements

Those chunks get ingested in an outer loop that goes through the timesteps, and then in the output values loop.

As a take-home message, Rayon is very helpful in splitting inputs into parallelised chunks, and each batch’s computation is independent so that everything can be computed in parallel. Again, we’re exploiting sequential data access and working on contiguous blocks of memory.

My best approach: Blas

The final approach I tested is using Blas. Blas is natively written in Fortran, but it has Rust bindings. It offers several approaches for mathematical computations, one of them is sgemm, which performs matrix multiplication in single precision (single-precision GEeneral Matrix Multiply), according to the formula:

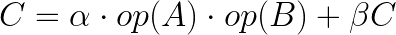
Here, A is a M x K matrix, B is K x N, and C is M x N — the output matrix. The parameters alfa and Berta are single-precision floats or “scalars”, so they are matrix multipliers. op is an operation on a given matrix so that we can have either the transpose or the complex conjugate. In coding terms, the matrix multiplication can be defined as:

fn matmul_blas(
    out: &mut [f32],
    inp: &[f32],
    weight: &[f32],
    bias: Option<&[f32]>,
    b: usize,   
    t: usize,  
    c: usize,   
    oc: usize, 
) {
    // inp size: m x k = ( (BT) x C) 
    // weight size: n x k = (OC x C) --> transposed (C x OC) 

    let m = (b * t) as i32; // output rows for C
    let k = c as i32;    // number of columns for A and rows for B
    let n = oc as i32;   // number of columns for C

    // Leading dimensions for Row-Major layout
    let lda = k; // lda >= K
    let ldb = k; // ldb >= N
    let ldc = n; // ldc >= N


    unsafe {
        sgemm(
            Layout::RowMajor,
            Transpose::None, // Transpose of A ('N' for no transpose)
            Transpose::Ordinary, // Transpose of B
            m,
            n,
            k,
            1.0,
            inp,
            lda,
            weight,
            ldb,
            0.0,
            out,
            ldc,
        );
    }

    // Add bias if present
    if let Some(bias) = bias {
        out.par_chunks_mut(oc)
            .for_each(|row| {
                for (o, val) in row.iter_mut().enumerate() {
                    *val += bias[o];
                }
            });
    }
}

The sgemm needs the following:

• Layout::RowMajor means we are storing our input matrices in row major order, so the consecutive elements of a row reside next to each other
• transa: Transpose::None here the input is matrix A, None specifies we do not want this matrix to be transposed
• transb: Transpose::Ordinary means that matrix B will be transposed
• m is the number of rows in the resulting matrix C, that’s b*T
• n is the number of columns we have in C, oc
• k is the shared dimension, so it’s the number of channels c that’s the number of columns in the input matrix A
• alpha=1.0 is the first scalar, in our case is 1
• a=inp is the input matrix
• lda this is the leading dimension in the array A. Since we are in RowMajor order, and not transposing, this corresponds to the number of columns of A;
• weight represents our matrix B
• ldb is the leading dimension for matrix B, that’s k as well
• beta=0.0 as we do not need beta in our calculation
• out is the matrix C
• ldc the leading dimension for C, that’s naka the number of columns in our output

If we combine this with eq.4 it’s easy to see we’re computing matrix A times the transposed of B.

From the Rust perspective we can see unsafe and what’s this? Now Rust is designed to be memory-safe by default, to prevent errors such as null pointers dereferencing. The unsafeblock allows the user to tell the Rust compiler “Watch out, this may not be safe, but do not worry”. unsafe is needed here, as we’re using sgemm that works as a function that’s interfacing via bindings, or through the “Foreign Function Interface” (FFI). It’s thus our responsibility to pass valid pointers, with checks on lengths and sizes. Thus, we could add some assertions in our code such as:

assert!(inp.len() >= (b * t * c), "Input slice is too small.");
assert!(weight.len() >= (oc * c), "Weight slice is too small.");
assert!(out.len() >= (b * t * oc), "Output slice is too small.");

for ensuring input matrices have lenghts that are at least as large as needed, and checks on null pointers too

assert!(!inp.is_empty(), "Input slice is empty.");
assert!(!weight.is_empty(), "Weight slice is empty.");
assert!(!out.is_empty(), "Output slice is empty.");

Conclusions

I think we crunched many details for today’s post. In this article I wanted share my lessons learned in finding the best way to implement the matrix multiplication operation in Rust, to get to a code similar to Karpathy’s llm.c

In this article we explored:

• A naive implementation in C with OpenMP
• Compare OpenMP performance with Rust performance. The comparison was done with a batch size B=64, a timestep T=1024, a channel size and output channel size C and OC = 768. In particular, I walked you through:

1. A simple translation of the C code to Rust. Here, we appreciated the pointer arithmetic and how simple a possible conversion from C to Rust is.
2. The usage of a more powerful crate, Rayon. The attention here was to create chunks from the output and input array and work in parallel with these chunks so that we could run independent processes and speed up the overall calculation. If we see tab.1, Rayon takes about 4s for processing forward and backward multiplication;
3. How to implement a matrix multiplication with Blas in Rust, to achieve even a better performance. Blas resulted as the best approach, with millisecond benchmarks. Moreover, fig. 1 and fig.2 show how forward and backward multiplication performs for different input/output sizes, ranging from B=4...128 , T=64... 2048, and C / OC = 48...1536.

From these conclusions, we can move forward with the creation of the llm.rust project, writing matrix multiplications in Blas. Let’s meet us in the next post, where we’ll go another step ahead in the writing up of this code :) . Thanks very much for following me. For any question, feel free to write a comment or write to stefanobosisio1@gmail.com

---

Writing LLMs in Rust: Looking for an Efficient Matrix Multiplication was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

from Datascience in Towards Data Science on Medium https://ift.tt/pnEXlqy
via IFTTT