Datascience in Towards Data Science on Medium,

A Case for Bagging and Boosting as Data Scientists’ Best Friends

12/17/2024 Jesus Santana

Leveraging wisdom of the crowd in ML models.

In recent years, we take resources such as Wikipedia or Reddit for granted — these resources rely on the collective knowledge of individual contributors to serve us with mostly accurate information, which is sometimes called the “wisdom of the crowd”. The idea is that the collective decision can be more accurate than any individual’s judgement, since we can each have our own implicit biases and/or lack of knowledge, resulting in some level of error in our judgement. Collectively, these errors might be offset by each other — for example, we can compensate for someone else’s lack of knowledge/expertise in one area, while they would make up for ours in other areas. Applying this idea to machine learning results in “ensemble” methods.

At a very high level, we train machine learning models in order to make predictions about the future. In other words, we provide the models with the training data with the hope that model can make good predictions about the future. But what if we could train several machine learning models and then somehow aggregate their opinions about the predictions? It turns out, this can be a very useful approach, which is widely used in the industry.

In this post, we will walk through the most common ensemble methods called bagging and boosting and implement a some examples to learn how they work in practice. Then we will talk about other more advanced ensemble methods.

Ensemble methods can be used for various machine learning approaches and for this post I have selected decision trees as our model of choice for a few reasons:

1. Practicality: Decision trees are widely used in the industry.
2. Understandability: Decision trees are easy to understand since we can visualize them and look at how they work.
3. Error Handling: Decision trees can overfit rather easily, which helps us demonstrate how to troubleshoot and improve the model, once such errors happen.

Before getting into the details, let me summarize what we will cover today in a table that you can use for your future reference. My recommendation is to save this table and use it in the future when you are thinking of what bagging and/or boosting approach to use for a given task.

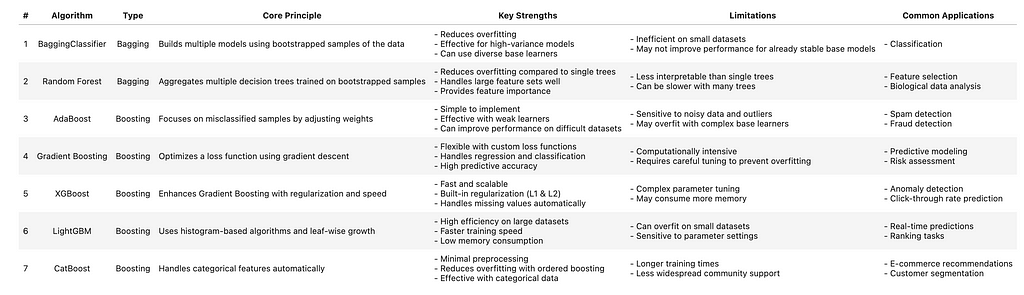
With the introductions out of the way, let’s start by bagging first.

1. Bagging

The first technique that we will cover is called bagging, which is short for Bootstrap Aggregating. It is an ensemble technique that trains multiple models on different subsets of the data and then aggregates their predictions. In general, bagging includes happens in three steps as follows:

1. Bootstrap Sampling: Create multiple subsets of the original dataset, usually done by sampling with replacement. Sampling with replacement means that once a sample (i.e. subset) is randomly collected from the original data set, the sample is put back in the data set, before the next sample is drawn. In other words, these subsets can have overlapping data. This type of sampling is called “bootstrap” because it is done with replacement.
2. Model Training: Train a base model, such as a decision tree, on each subset.
3. Aggregation: Combine the predictions of all models. This can be done through majority vote for classification, average for regression or other methods.

Now that we understand how bagging is done, let’s talk about the benefits we can expect from this technique.

1.1. Bagging — Benefits

With the above explanation, we now understand what bagging means but why would we use bagging? Bagging provides the following benefits:

1. Improve Accuracy: Individual models may make errors, but when we combine them, their predictions tend to correct each other’s mistakes.
2. Reduce Variance: Since we train multiple models on different subsets of the data and average their predictions (or taking a majority vote in classification), bagging reduces the impact of any single model’s overfitting to its specific subset and therefore reduces variance. This results in an overall system that generalizes better than a single model.
3. Efficiency: Since each of the individual models in bagging is trained independently on different bootstrapped samples (i.e. subset of the data), the training process can be parallelized, making it computationally efficient.

1.2. Bagging — Implementation

Now that we understand what bagging is, let’s implement a simple example to compare how it can improve the performance of our training process. In order to do so, we will train three separate models for this exercise (further explained below) and compare their performance by calculating accuracy. Accuracy measures the proportion of correct predictions made by the model out of all predictions. It is calculated as follows:

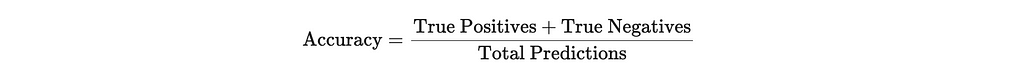
Evaluation of ML models is a foundational knowledge for all machine learning practitioners but it is outside of the scope of this post. If you are interested in learning more about evaluation and various metrics used for evaluation of machine learning systems, refer to the post below, which has a specific section dedicated to evaluation of models.

Machine Learning Basics I Look for in Data Scientist Interviews

In order to better understand the implementation and the models that we will be using, I will break it down into four steps, as follows:

1. Datasets: First we create a synthetic dataset for a binary classification exercise. It is called binary meaning that there are only two classes (e.g. 0 or 1). Then we break the data set down into train and test sets. Train set is what is used to train the models and test set will be used for evaluation of the trained models.
2. Single Decision Tree: This will be our baseline. We first train a single decision tree to see how a single decision tree performs. Then we will create more sophisticated models and compare their performance to the single decision tree.
3. Bagging Classifier: In this step, we create a bagging classifier and calculate its performance. Based on our discussion so far, we expect this to be better than the single classifier. Fingers crossed!
4. Random Forest Classifier: I also wanted to include a random forest classifier here for comparison, which is a specific type of bagging strategy to lower likelihood of overfitting.

Let’s implement the code and look at the results!

# import libraries
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier, RandomForestClassifier
from sklearn.metrics import accuracy_score

# step 1: create a synthetic dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=1234)

# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=1234)

# step 2: a single decision tree
# initialize a decision tree classifier (dtc)
dt_clf = DecisionTreeClassifier(random_state=1234)

# train the dtc
dt_clf.fit(X_train, y_train)

# predict using trained dtc
y_pred_dt = dt_clf.predict(X_test)

# evaluate using accuracy
accuracy_dt = accuracy_score(y_test, y_pred_dt)
print(f"Decision Tree Accuracy: {accuracy_dt * 100:.2f}%")

# step 3: a bagging classifier
# initialize a bagging classifier
bagging_clf = BaggingClassifier(estimator=DecisionTreeClassifier(), n_estimators=100, random_state=1234)

# train
bagging_clf.fit(X_train, y_train)

# predict
y_pred_bagging = bagging_clf.predict(X_test)

# evaluate
accuracy_bagging = accuracy_score(y_test, y_pred_bagging)
print(f"Bagging Classifier Accuracy: {accuracy_bagging * 100:.2f}%")

# step 4: a random forest classifier
# initialize a random forest classifier
rf_clf = RandomForestClassifier(n_estimators=100, random_state=1234)

# train
rf_clf.fit(X_train, y_train)

# predict
y_pred_rf = rf_clf.predict(X_test)

# evaluate
accuracy_rf = accuracy_score(y_test, y_pred_rf)
print(f"Random Forest Classifier Accuracy: {accuracy_rf * 100:.2f}%")

Results:

As we can see in the results, the single decision tree had an accuracy of 84.0%. Introducing bagging, increased the accuracy to 92.4%, which is a considerable improvement. Random forest also performed very well at 92.0% but not as good as the bagging classifier. As expected, we see that using a bagging strategy can result in a significant improvement in the performance of the trained model.

That covers the bagging introduction. Next, we will talk about boosting!

2. Boosting

Boosting is another ensemble technique that converts weak learners (i.e. models) into strong learners by iteratively improving model performance. As you recall, bagging focuses on combining the prediction of models but unlike bagging, boosting focuses on correcting the errors made by previous models, allowing each subsequent model to learn from the mistakes of the prior ones.

Boosting is usually done through the following steps:

1. Sequential Training: Models are trained one after another in a sequence, where each new model aims to correct the errors made by the previous models. This is the main difference between bagging and boosting. As you recall, in bagging, training of different models can happen in parallel, while in boosting, trainings are sequential.
2. Focused Improvement: During training, more weight is assigned to data points that were previously misclassified, forcing the new model to focus more on the harder cases. This is the step that hopefully will result in “boosted” or improved performance, which is why this technique is called boosting.
3. Aggregation: Once we have gone through the sequential training and focused improvement, the predictions of all models are combined, often with weights based on each model’s performance. This weighted combination helps form a stronger overall prediction.

We now understand conceptually what boosting is so let’s look at some of the benefits of boosting next.

2.1. Boosting — Benefits

Similar to our discussing about bagging, in this section we will talk about some of the benefits of using boosting techniques.

1. Improve Accuracy: Boosting is a technique to improve the accuracy of our predictions, since each learner focuses on correcting the mistakes of the previous ones, leading to highly accurate predictions.
2. Reduce Bias: Boosting reduces bias by iteratively improving upon the predictions of earlier models. Note that bagging was good at reducing variance (i.e. overfitting), while boosting is more suited for reducing bias (i.e. underfitting).
3. Outlier Handling: Boosting algorithms naturally give more weight to difficult or misclassified examples, allowing the model to pay extra attention to outliers and therefore this technique is generally very good at handling outliers.
4. Versatility: Boosting can be used for both regression and classification tasks, making it a versatile tool for machine learning practitioners.

Now that we understand what boosting is and the benefits of using the technique, let’s talk about a few boosting algorithms.

2.2. Boosting — Algorithms

There are various boosting algorithms available and in this section we are going to go over some of the most commonly-used ones.

1. AdaBoost: Stands for Adaptive Boosting and starts by training a weak learner on the original data set and assigns training data equal weights initially. Then it reiterates and increases the weight of the misclassified samples and as a result the following learner focuses mainly on the misclassified and presumably more difficult samples. The process continues and the final prediction is a weighted combination of all weak learners. This approach is very similar to how we described boosting in general and is a relatively simple implementation of boosting idea, which makes it a good starting point for us. Next approaches will get more sophisticated.
2. Gradient Boosting: Similar to adaptive boosting, is also an iterative approach but this method builds the models by optimizing a loss function. The loss function can be a metric such as mean squared error for regression or log-loss for classification problems. Each sequential learner is trained to minimize the error directly, unlike the adaptive boosting, which focused on adjusting sample weights instead.
3. XGBoost: This is probably my favorite boosting algorithm and I have a full article that focuses on this topic (linked below) but let’s provide a high-level overview here. XGBoost stands for Extreme Gradient Boosting. As the name suggests, this is also a gradient boosting approach but it adds regularization to better manage overfitting, which makes it a powerful algorithm. XGBoost also supports parallelization, which enables shorter training time, and handles missing values in the data sets very well. All these positive attributes, make XGBoost a powerhouse when it comes to various problems. Article below covers XGBoost and its implementation in more details.

XGBoost: Intro, Step-by-Step Implementation, and Performance Comparison

4. LightGBM: Which stands for Light Gradient Boosting Machine, splits trees leaf-wise, instead of level-wise. Let me explain what this means. Each decision tree starts with a node and then it is split into the next level nodes through branches. So branches connect the node to its next level nodes. For example, if we want to split a node into two categories, then there will be two branches, connecting the first node to the next level nodes. In traditional methods, the tree grows level-wise, meaning that once we get to a new set of nodes in a level, each of those nodes are then split into as many branches as exists at that level. but in the LightGBM case, it does not split all the nodes at each level. Therefore, LightGBM is more efficient for larger data sets. Let me visualize this in an example so that we can more easily understand it.

For this example, you do not need to follow the code but I will include the code I used to generate the trees. We will run the code and then explain the difference between the LightGBM and traditional approaches.

# import libraries
import matplotlib.pyplot as plt
import networkx as nx
import heapq

# function to create tree structure
def create_tree_structure(levels, leaf_wise=False):

    G = nx.DiGraph()
    G.add_node("Root")
    G.nodes["Root"]["split"] = False
    node_count = 1

    if not leaf_wise:
        # level-wise growth
        current_level_nodes = ["Root"]
        for level in range(levels):
            next_level_nodes = []
            for node in current_level_nodes:
                left_child = f"N{node_count}"
                node_count += 1
                right_child = f"N{node_count}"
                node_count += 1
                G.add_edge(node, left_child)
                G.add_edge(node, right_child)
                G.nodes[node]["split"] = True  # mark this node as split
                G.nodes[left_child]["split"] = False
                G.nodes[right_child]["split"] = False
                next_level_nodes.extend([left_child, right_child])
            current_level_nodes = next_level_nodes
    else:
        # leaf-wise growth
        G.nodes["Root"]["split"] = False
        max_splits = levels
        splits = 0

        # heap to select the leaf with the highest gain
        # heap elements are (-gain, depth, node_id)
        heap = [(-100, 0, "Root")]
        while splits < max_splits and heap:
            neg_gain, depth, node = heapq.heappop(heap)
            if depth >= levels:
                continue
            left_child = f"N{node_count}"
            node_count += 1
            right_child = f"N{node_count}"
            node_count += 1
            G.add_edge(node, left_child)
            G.add_edge(node, right_child)
            G.nodes[node]["split"] = True
            G.nodes[left_child]["split"] = False
            G.nodes[right_child]["split"] = False
            # assign arbitrary and decreasing gains to the new leaves
            new_gain = neg_gain + 10  # decrease gain for deeper nodes
            heapq.heappush(heap, (new_gain, depth + 1, left_child))
            heapq.heappush(heap, (new_gain + 1, depth + 1, right_child))
            splits += 1
    return G

# visualizing function
def plot_tree(tree, title, ax):
    pos = nx.nx_agraph.graphviz_layout(tree, prog="dot")
    nx.draw(tree, pos, with_labels=True, arrows=False, node_size=2000, ax=ax)
    nx.draw_networkx_nodes(
        tree, pos, 
        nodelist=[n for n in tree.nodes if tree.nodes[n].get("split", False)],
        node_color="red", ax=ax)
    ax.set_title(title)

levels = 4
tree_level_wise = create_tree_structure(levels, leaf_wise=False)
tree_leaf_wise = create_tree_structure(levels, leaf_wise=True)

# plot
fig, axs = plt.subplots(1, 2, figsize=(15, 10))
plot_tree(tree_level_wise, "Level-wise Tree Growth (Traditional)", axs[0])
plot_tree(tree_leaf_wise, "Leaf-wise Tree Growth (LightGBM)", axs[1])
plt.tight_layout()
plt.show()

Results:

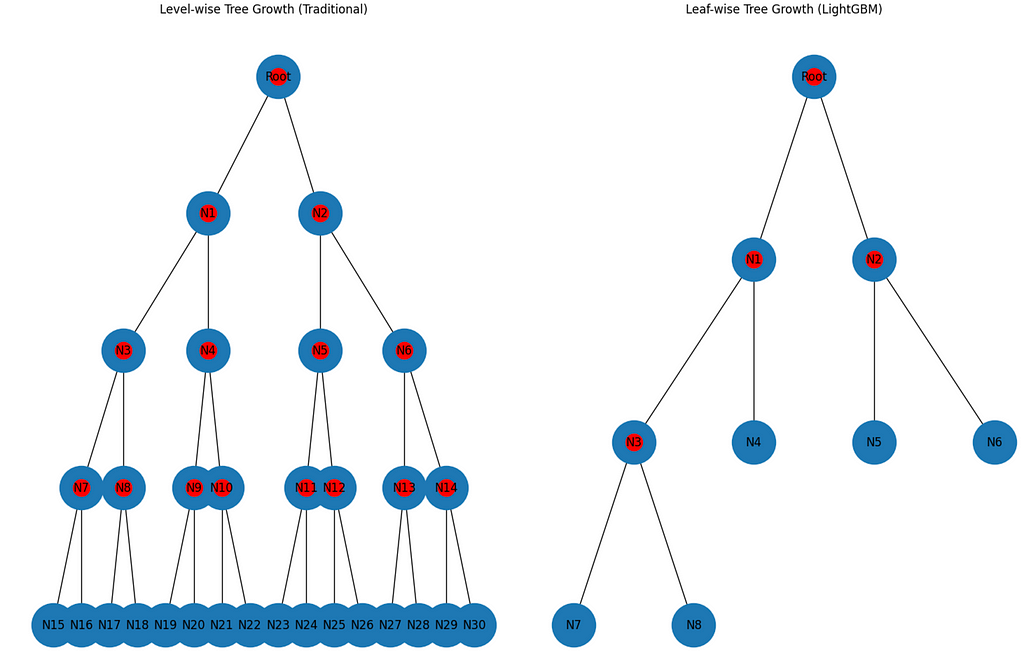
As we can see from the plot above, the LightGBM approach only splits certain nodes (the ones with a red dot in the image), that the algorithm expects will have the highest potential for error reduction and therefore makes this much more efficient than the traditional approaches.

Let’s cover one more boosting algorithm and then we will get to the fun part of implementation.

5. CatBoost: As you might have guessed by the name, CatBoost is optimized for categorical features, and hence the “Cat” in the name, without the need for an extensive preprocessing and data cleaning. It has some optimizations internally, such as ordered boosting, which helps reduce overfitting and is considered one of the more efficient boosting algorithms.

Now that we are more familiar with some of the boosting algorithms, we will implement and compare the performance of these models to learn them in practice.

2.3. Boosting — Implementation

In this part, we are going to put what we have learned so far about boosting to test. For this exercise, we are going to use the breast cancer data set that is publicly available through the scikit-learn library, which is taken from UC Irvine’s Machine Learning Respository, available under a CC BY 4.0 license. This is a binary classification data set, commonly used to demonstrate the implementation and performance of various classification algorithms.

I have selected one decision tree without bagging or boosting as the baseline, followed by two boosting algorithms, which are AdaBoost and gradient boosting and then I compare the results to random forest, which is a bagging algorithm. We will first load the data, train our models and then compare their performance using two evaluation metrics of accuracy and area under curve. We defined accuracy earlier in the post as the ratio of correctly predicted observations to the total observations in the data set so let’s define what the area under curve is. Area Under the Receiver Operating Characteristic Curve or AUC-ROC represents the ability of the model to distinguish between the positive and negative classes.An AUC-ROC of 0.5 suggests no discrimination between positive and negative classes — in other words, the model is no better than random selection between positive and negative classes. A value larger than 0.5 suggests some discrimination between the two classes is happening and 1 is the perfect discrimination. In short, a higher AUC-ROC indicates a better model performance.

Now that we know the process and are familiar with the evaluation metrics, let’s implement and look at the results.

# import libraries
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, roc_auc_score
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier, GradientBoostingClassifier, RandomForestClassifier
import warnings

warnings.filterwarnings("ignore")

# load the dataset
data = load_breast_cancer()
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target

# feature scaling
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# train-test split
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=1234, stratify=y
)

# initialize models
# decision tree
dt_clf = DecisionTreeClassifier(random_state=1234)

# adaboost
ada_clf = AdaBoostClassifier(
    estimator=DecisionTreeClassifier(max_depth=1),
    n_estimators=50,
    learning_rate=1.0,
    random_state=1234,
)

# gradient boosting
gb_clf = GradientBoostingClassifier(
    n_estimators=100, learning_rate=0.1, max_depth=3, random_state=1234
)

# random forest
rf_clf = RandomForestClassifier(
    n_estimators=100, max_depth=None, random_state=1234
)

# train
dt_clf.fit(X_train, y_train)
ada_clf.fit(X_train, y_train)
gb_clf.fit(X_train, y_train)
rf_clf.fit(X_train, y_train)

# predict
y_pred_dt = dt_clf.predict(X_test)
y_proba_dt = dt_clf.predict_proba(X_test)[:, 1]

y_pred_ada = ada_clf.predict(X_test)
y_proba_ada = ada_clf.predict_proba(X_test)[:, 1]

y_pred_gb = gb_clf.predict(X_test)
y_proba_gb = gb_clf.predict_proba(X_test)[:, 1]

y_pred_rf = rf_clf.predict(X_test)
y_proba_rf = rf_clf.predict_proba(X_test)[:, 1]

# evaluate
results = pd.DataFrame(
    {
        "Algorithm": [
            "Decision Tree",
            "AdaBoost",
            "Gradient Boosting",
            "Random Forest",
        ],
        "Accuracy": [
            round(accuracy_score(y_test, y_pred_dt), 4),
            round(accuracy_score(y_test, y_pred_ada), 4),
            round(accuracy_score(y_test, y_pred_gb), 4),
            round(accuracy_score(y_test, y_pred_rf), 4),
        ],
        "ROC AUC": [
            round(roc_auc_score(y_test, y_proba_dt), 4),
            round(roc_auc_score(y_test, y_proba_ada), 4),
            round(roc_auc_score(y_test, y_proba_gb), 4),
            round(roc_auc_score(y_test, y_proba_rf), 4),
        ],
    }
)

print(results)

Results:

Let’s discuss the results. While decision tree is simple and performs reasonably well with an accuracy of 96.5% and an ROC AUC of 96.7, it is outperformed by the remaining ensemble methods overall, although its accuracy is higher than AdaBoost’s. AdaBoost performs well, especially in terms of ROC AUC (99.5%), but its accuracy (95.6%) is slightly lower than other methods. Gradient boosting is the best-performing model overall, with the highest accuracy (97.4%) and ROC AUC (99.9%). Random forest performs slightly better than gradient boosting in terms of ROC AUC (99.9%) but has slightly lower accuracy (96.5%).

Conclusion

In this post, we talked about two of the most commonly-used ensemble methods of bagging and boosting. We talked about how smaller and or weaker models are combined to create more powerful systems and therefore improve the overall performance. We then implemented and compared the performance of these bagging and boosting methodologies.

Thanks For Reading!

If you found this post helpful, please follow me on Medium and subscribe to receive my latest posts!

(All images, unless otherwise noted, are by the author.)

---

A Case for Bagging and Boosting as Data Scientists’ Best Friends was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

from Datascience in Towards Data Science on Medium https://ift.tt/fMRyIXG
via IFTTT