Chi-Squared Test: Comparing Variations Through Soccer
Understanding Different Types of Chi-Squared Tests: A/B Testing for Data Science Series (11)

If you are not a paid member on Medium, I make my stories available for free: Friends link
The term “Chi-Squared Test” is often thrown around without much clarification about which specific test is being referenced. Of course, if you are a data scientist, you should know type of test that the other is referring to. However, if you are someone just jumping into their data science career or learning about data science, it’s pretty understandable that this distinction can be confusing.
That’s exactly why I’m writing this article today!
I’ll help you break down the different types of Chi-Squared tests and provide a thorough explanation of when and how to use them. This article will be a continuation of my A/B Testing and Hypothesis Testing series, so if you are interested, go check them out as well!
Also… Before I start getting into the details, I want to take a moment to acknowledge the timing of this article. As my final writing for 2024, I imagine many of you might be reading this on New Year’s Eve, New Year’s Day, or sometime shortly after.
I hope 2024 has been a fantastic year for you, and I wish you all an incredible 2025 ahead.
It’s been a great journey so far and I am excited to write more great articles in 2025! With that said, let’s get started into the last article of the year!
Note: Please skip to the second section if you know the basics of a Chi-Squared Test already!
Table of Contents
- Chi-Squared Test
- Analyzing Playing Styles in Serie A: Chi-squared test for Independence
- Penalty Kick Success Rate: Chi-Squared Test for Homogeneity
- Goals Scored in Soccer Matches: Chi-Squared Test for Goodness-of-Fit
- Summary
Chi-Squared Test
The Chi-Squared Test is a statistical method used to help us figure out whether the differences (or similarities) we observe between categorical variables happen by chance or reflect a real, meaningful relationship. This makes it an essential tool in hypothesis testing, widely used in data science and other fields.
If you recall, categorical variables are types of variables in data that represent groups or categories instead of numerical values.
To identify whether something is a categorical variable or not, I generally ask myself “Does this have a finite set of distinct groups?” For instance, if we’re analyzing “preferred drink choices” in a survey, the options might be categories like coffee, tea, water, soda, or juice. Since I can clearly list these distinct groups, I know it’s a categorical variable.
Types of Chi-Squared Tests
There are three main types of Chi-Squared Tests, each serving a specific purpose:
- Chi-Squared Test for Independence determines if there is a significant association between two categorical variables in a single population.
- Chi-Squared Test for Homogeneity compares the distribution of a categorical variable across two or more different populations or groups.
- Chi-Squared Goodness of Fit Test determines whether the observed distribution of a single categorical variable matches a theoretical or expected distribution.
If this seems confusing, don’t worry! I’ll break down each type of test with detailed examples to make it clearer.
Key Concepts
Chi-Squared Test is a hypothesis-testing method
- Null Hypothesis (H₀): Assumes no significant relationship or difference exists.
- Alternative Hypothesis (Hₐ): Assumes a significant relationship or difference exists.
- Right-Tailed: The Chi-Squared Test is always right-tailed because the test statistic (χ²) is based on squared differences, which are always positive. Large values of χ² indicate significant deviations from the null hypothesis, leading to its rejection.
- Contingency Table: Generally for the chi-squared test for independence, you’ll see some sort of a table that shows the data for each categorical variable (like the one below). It summarizes the data to understand the relationship between the variables.
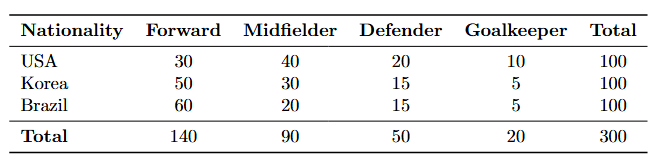
If these concepts seem complex, don’t worry! In the next sections, I’ll explain Chi-squared with a concrete example and go over each type of Chi-Squared Test in detail, so you can confidently apply them to your own data analyses.
Now that we’ve covered the basics, let’s use one of my favorite topics — soccer — to illustrate this test. For my readers who have been following my articles, you know I love to use soccer!

Analyzing Playing Styles in Serie A: Chi-squared test for Independence
Imagine you are working with AC Milan’s head coach as a data scientist. You and the head coach have been hired by the team with a new season coming up (2025–2026). AC Milan has been known for their strong defensive style of football. However, this approach hasn’t been very successful in recent years.
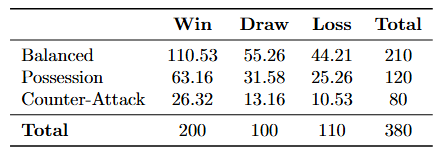
With a new season on the horizon, the coach is curious to understand whether certain playing styles — such as Balanced, Possession-based, or Counter-Attack — are associated with better match outcomes (Win, Draw, or Loss) across Serie A teams.
To test this, you analyze match results from the entire past Serie A season (2024–2025). This data represents a single population: all matches played in Serie A that season. You’re examining the relationship between two categorical variables:
- Playing Style: Balanced, Possession, Counter-Attack.
- Match Result: Win, Draw, Loss.
For simplicity, the dataset for our hypothetical Serie A analysis is summarized in the table below.
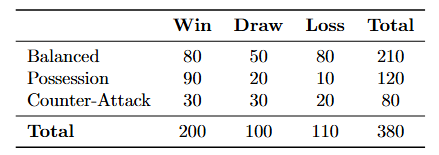
Note for readers: While real-world match outcomes are influenced by various factors — like squad depth, player availability, and injuries — we’ll focus solely on playing style for this analysis!
Define the Hypothesis
How can we use a statistical test to determine whether certain playing styles influence match results? Well… remember that this is a hypothesis test, so let’s define the null and alternative hypotheses!
- Null Hypothesis (Hₒ): Playing style is independent of match result. (No relationship exists between playing style and outcome.)
- Alternative Hypothesis (Hₐ): Playing style is associated with match result. (A relationship exists between the two variables.)
To test these hypotheses, we’ll use the Chi-Squared Test for Independence to evaluate whether the observed differences in match results are statistically significant!
What do we expect from our data?
Before we begin performing the test… let’s take a step back and consider what the Chi-Squared Test for Independence is trying to achieve. At its core, it’s safe to say that this test asks:
- Are the differences in match results across playing styles just random?
- Or do these differences reflect a meaningful relationship between playing style and outcomes?
Now, let’s consider this intuitively.
If playing style has no impact on match results, the number of wins, draws, and losses for each style should align with the overall proportions in the data. For example, if 50% of all matches result in a win, we’d expect each playing style to have roughly 50% wins!
If we were to calculate the expected data for each correlation of playing style to match results… It can simply be calculated based on the row and column totals.
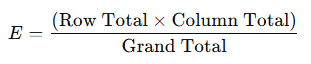
For example, the expected number of wins for the Balanced playing style is shown below. We can do the same for every single cell to get the expected data!
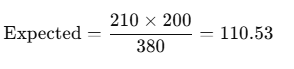
Why Does This Matter?
Okay, we intuitively went over what we expect our data to be. But, why do we care about the expected data instead of just looking at the observed data?
Well…! The expected data is critical to our Chi-Squared Test because it serves as the baseline for comparison. By calculating the expected values, we essentially say:
- “If playing style has no impact on match results (i.e., no relationship exists), this is what the data should look like.”
When we compare the observed to the expected data, any significant deviation might indicate that playing style and match results are related.

It makes sense, right? If there’s truly no relationship, the observed data should closely align with the expected data. On the other hand, if the observed data is notably different from the expected, it suggests that a relationship might exist between playing style and match outcomes.
Understanding the Chi-Squared Test
This comparison is the foundation of the Chi-Squared Test, helping us determine whether the differences are statistically significant or just random chance.
The key metric in this test is the Chi-Squared statistic (χ²), which measures how much the observed data deviates from the expected data, assuming the two variables are independent. The formula for calculating the Chi-Squared statistic is:
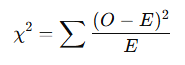
- O is the observed frequency in each cell of the contingency table.
- E is the expected frequency in each cell of the contingency table.
For each cell in the table, you calculate this value and then sum them all up to get the total Chi-Squared statistic!
Performing the Test Using Python
Now, you can use Python to calculate the Chi-Squared statistic and determine whether the observed differences are statistically significant! We’ll set the significance level (α) to 0.05.
import numpy as np
from scipy.stats import chi2_contingency
# Observed data
observed = np.array([
[80, 50, 80], # Balanced
[90, 20, 10], # Possession
[30, 30, 20] # Counter-Attack
])
# Perform Chi-Squared Test
chi2, p_value, dof, expected = chi2_contingency(observed)
# Results
print("Chi-Squared Statistic:", chi2) # 72.34
print("P-Value:", p_value) # 0.00001
print("Degrees of Freedom:", dof) # 4
print("Expected Frequencies:\n", expected) # Table for expected values
# Significance level
alpha = 0.05
By looking at our data, we got a p-value of 0.00001, which is less than the significance level (α=0.05). What does this mean? It means that we reject the null hypothesis. This indicates a statistically significant relationship between playing style and match outcomes in Serie A.
So we can say to the head-coach that we can explore adopting a Possession-based style, as it shows a stronger association with better match results (e.g., more wins) based on the analysis!
Applying Chi-Squared Tests in Different Scenarios
We just went over the chi-squared test for independence and how it works! Luckily, for all types of Chi-Squared tests — whether it’s the Chi-Squared Test for Homogeneity or the Chi-Squared Goodness-of-Fit Test — the foundational calculations remain the same as those used in the Chi-Squared Test for Independence!
- Start with the observed data.
- Calculate the expected data.
- Compute the Chi-Squared statistic.
- Evaluate its statistical significance.
Pretty simple right!!?
Since the procedures are very similar across these tests, for the other types of Chi-Squared tests… I’ll focus on the scenarios where each test is used instead of going into the details again!

Penalty Kick Success Rate: Chi-Squared Test for Homogeneity
For a data science project, I analyzed data on the success rates of penalty kicks — categorized as Goal, Saved, or Missed — from various high-profile soccer tournaments, including the UEFA Champions League, FIFA World Cup, and Copa América.
The goal of this project was to investigate whether the success rates of penalty kicks differ across these tournaments or remain consistent, considering the varying levels of pressure and competition in each event.
Interesting right?
This kind of question is perfect for solving with the Chi-Squared Test for Homogeneity! Remember that in this variation of the Chi-Squared test you are looking to compare whether the distribution of a categorical variable (success rate of penalty kicks) is the same across multiple groups or populations (different soccer tournaments).
Below is the data, try out the Chi-Squared Test for Homogeneity yourself!

Answer
import numpy as np
from scipy.stats import chi2_contingency
# Observed data
observed = np.array([
[40, 35, 30], # Goal
[20, 25, 15], # Saved
[10, 15, 20] # Missed
])
# Perform the Chi-Squared Test
chi2, p_value, dof, expected = chi2_contingency(observed)
# Print results
print("Chi-Squared Statistic:", chi2)
print("P-Value:", p_value)
print("Degrees of Freedom:", dof)
print("Expected Frequencies:\n", expected)
# Chi-Squared Statistic: 7.688
# P-Value: 0.053
# Degrees of Freedom: 4
# Expected Frequencies:
[[35.0 37.5 32.5]
[20.0 21.43 18.57]
[15.0 16.07 13.93]]
# Fail to reject the null hypothesis: No significant difference in success rates across tournaments.

Goals Scored in Soccer Matches: Chi-Squared Test for Goodness-of-Fit
Imagine you want to test whether the distribution of goals scored in soccer matches aligns with a Poisson distribution. If you recall, the Poisson distribution is often used to model the number of events (like goals) occurring within a fixed interval, such as a single soccer match.
Probability Distributions: Poisson vs. Binomial Distribution
Based on historical league data, you hypothesize the following probability distribution for goals scored:
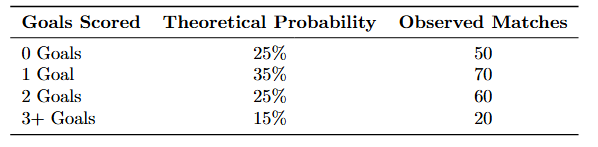
Observed Data and Theoretical Probability
This kind of question is perfect for solving with the Chi-Squared Test for Goodness-of-Fit! Remember that we use this variation to determine whether a single categorical variable (in this case, goals scored) follows a specific theoretical or expected distribution (e.g., Poisson).
By comparing the observed data with the theoretical probabilities, we can determine whether the two distributions are consistent or significantly different.
What this means is that unlike our previous variations of Chi-Squared Test, our hypothesis would be looking to see if the distribution of the categorical variable matches our theoretical distribution!
- Null Hypothesis (H₀): The observed distribution of goals matches the theoretical Poisson distribution.
- Alternative Hypothesis (Hₐ): The observed distribution of goals does not match the theoretical Poisson distribution.
Since it might be a bit confusing to calculate the expected data, I’ll provide you with it! Try out the Chi-Squared Test for Goodness-of-fit yourself!
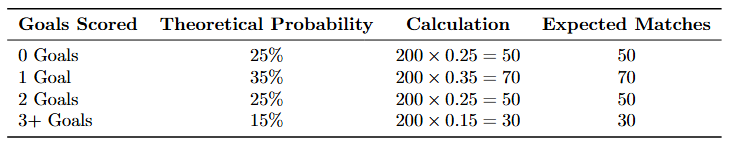
Answer
import numpy as np
from scipy.stats import chisquare
# Observed data
observed = np.array([50, 70, 60, 20])
# Expected data based on theoretical probabilities
expected = np.array([50, 70, 50, 30])
# Perform the Chi-Squared Goodness-of-Fit Test
chi2, p_value = chisquare(f_obs=observed, f_exp=expected)
# Print results
print("Chi-Squared Statistic:", chi2)
print("P-Value:", p_value)
# Chi-Squared Statistic: 1.8
# P-Value: 0.614
# Fail to reject the null hypothesis: The observed distribution matches the expected distribution.
Summary
Using soccer as a case study, we got to see how Chi-Squared Test for Independence can reveal relationships between variables, such as playing styles and match outcomes, enabling coaches to strategize more effectively.
Similarly, the Chi-Squared Test for Homogeneity helps compare distributions across groups, like penalty kick success rates in different tournaments.
And the Chi-Squared Goodness-of-Fit Test? It allows us to evaluate whether real-world data, such as goals scored in matches, aligns with a theoretical model, like the Poisson distribution, giving us better insights into game patterns and possible questions for further analysis.
I personally thought it was pretty confusing to understand the differences between the various types of Chi-Squared tests when I was learning them. My goal was to get these cleared up for you so you don’t struggle like I did (Well… I hope this article was able to do that for you).
I hope you were able to learn something!
Connect with me!
If you made it this far, I assume you are an aspiring data scientist, a teacher in the data science field, a professional looking to hone your craft, or just an avid learner in a different field! I would love to have a chat with you on anything!
For those wondering about my images: Unless otherwise noted, all images are by the author (myself)
Chi-Squared Test: Comparing Variations Through Soccer was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from Datascience in Towards Data Science on Medium https://ift.tt/AuMnoxL
via IFTTT




