Why Normalization Is Crucial for Policy Evaluation in Reinforcement Learning
Enhancing Accuracy in Reinforcement Learning Policy Evaluation through Normalization
Reinforcement learning (RL) has recently become very popular due to its use in relation to large language models (LLM). RL is defined as a set of algorithms centered around an agent learning to make decisions by interacting with an environment. The objective of learning process is to maximize rewards over time.
Each attempt by the agent to learn can affect the value function, which estimates the expected cumulative reward the agent can achieve starting from a specific state (or state-action pair) while following a particular policy. The policy itself serves as a guide to evaluate the desirability of different states or actions.
Conceptually the RL algorithm contains two steps, policy evaluation and policy improvement, which run iteratively to achieve the best attainable level of the value function. Within this post we limit our attention to the concept of normalization within policy evaluation framework.
Policy evaluation is closely related to the concept of state. A state represents the current situation or condition of the environment that the agent observes and uses to decide on the next action. The state is typically described by a set of variables whose values characterize the present conditions of the environment.
Policy evaluation is about figuring out how good a given strategy is by estimation the policy value function for each state.
The algorithm needs to calculate the expected rewards an agent can achieve if it starts in a certain situation and keeps following that policy. This helps to understand if the strategy is effective and can be used as a step toward making it better.
Normalization is often associated with the context of rarely visited states. It involves dividing metrics such as rewards or state values by the frequency of visits to those states. This approach helps to average the rewards per state and ensures a balance between frequently and infrequently visited states during the learning process, promoting more stable and equitable updates of value function.
Without normalization, policy evaluation risks bias, as rewards for rarely visited states can be unstable or disproportionately impact the learning process. By normalizing rewards by visit counts, we achieve a more representative average.
Notably, normalization is equally vital for frequently visited states, especially when comparing different environmental scenarios. We illustrate this concept using the game of Blackjack, a classic decision-making problem in RL often highlighted in research due to its limited state space.
Blackjack is a card game played against a dealer. We present the definition of the game after Barboianu (2022). At the start of a round, both player and dealer are dealt 2 cards. The player can only see one of the dealer’s cards. The goal of the game is to get the value of your cards as close to 21 as possible, without crossing 21. The cards are marked with different value: 10/Jack/Queen/King → 10; 2 through 9 → same value as the card; ace → 1 or 11 (Player’s choice). Note that ace is called useful when It can be counted as 11 without going over 21.
If the value of the player is less than 21, they can choose to “hit” and receive a random card from the deck. They can also choose to “stick” and keep the cards they have, without risking crossing the 21 mark. If the player exceeds 21, she loses the round. If the player has exactly 21, she wins automatically. Otherwise, the player wins if they are closer to 21 than the dealer.
There are two scenarios that can occur in the game, referred to as the usable ace and non-usable ace scenarios. An ace counts as 11 (non-usable ace scenario) unless doing so would cause the player’s total to exceed 21, in which case it counts as 1 instead (usable ace scenario).
These two scenarios are represented by separate value functions in the literature (including the seminal book by Sutton and Barto). The code attached to this post implements the Monte Carlo approach for policy evaluation (this methodology is well-documented in the aforementioned book).
The policy evaluated here assumes that both the dealer and the player decide whether to hit or stick based on some random threshold determined in their mind. This represents a slight modification of the more common policy, which assumes the player sticks at a fixed total of 20 and the dealer at 17.
The plot below depicts two surfaces, each corresponding to the value function for the usable ace and non-usable ace scenarios, respectively. Each state is represented by a pair (player total, dealer’s visible card).
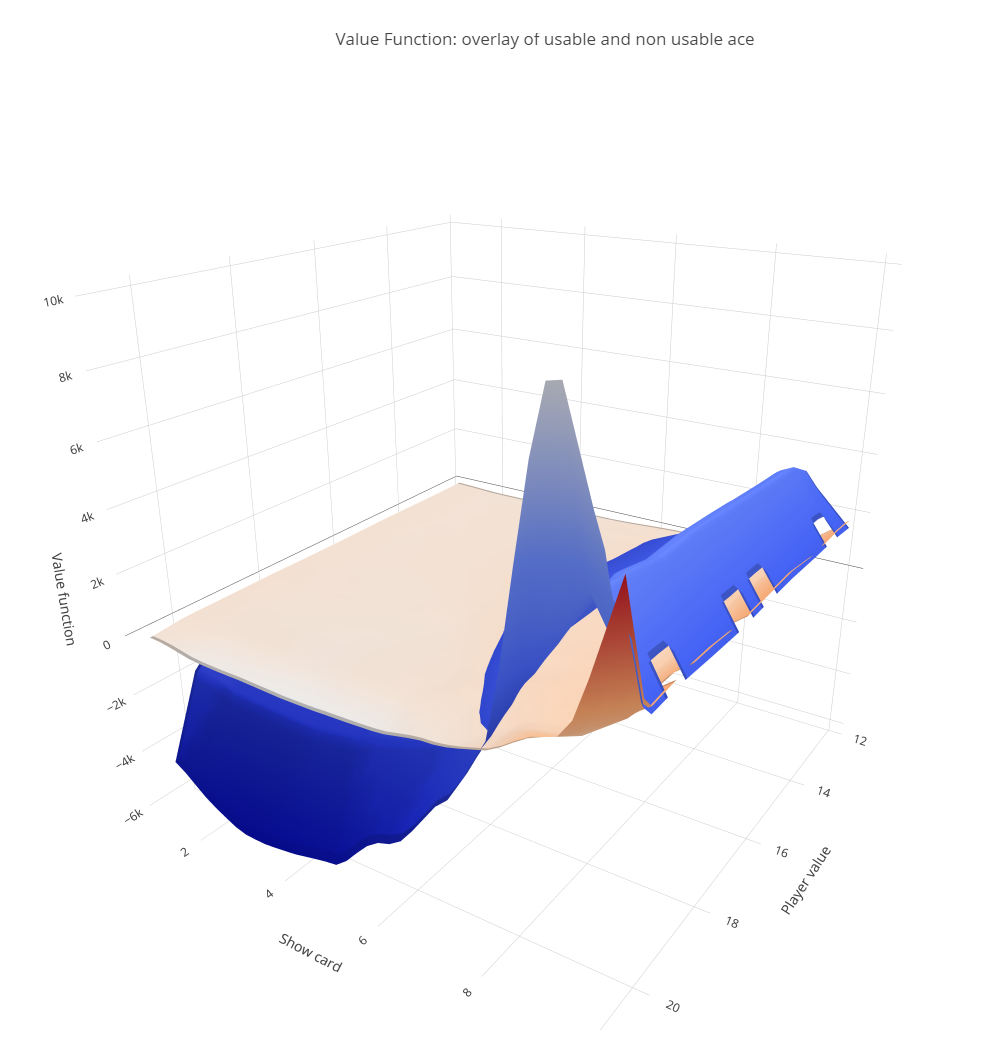
Interestingly, the non-usable ace surface (blue) is higher than the corresponding usable ace surface in the region where the dealer’s show card is high. This is counterintuitive, as the usability of an ace provides the player with more flexibility in decision-making and a higher probability of winning in this scenario compared to a non-usable ace, regardless of the state. So, where does this phenomenon come from?
Normalization proves useful in explaining this phenomenon. As mentioned in the introduction, the frequency of state visits plays a significant role in policy evaluation. In Blackjack, the value function is based on the number of times the player wins calculated over the total number of games played. However, this approach does not account for the fact that some states are visited far less frequently than others, simply because they are less likely to occur from the distributional viewpoint.
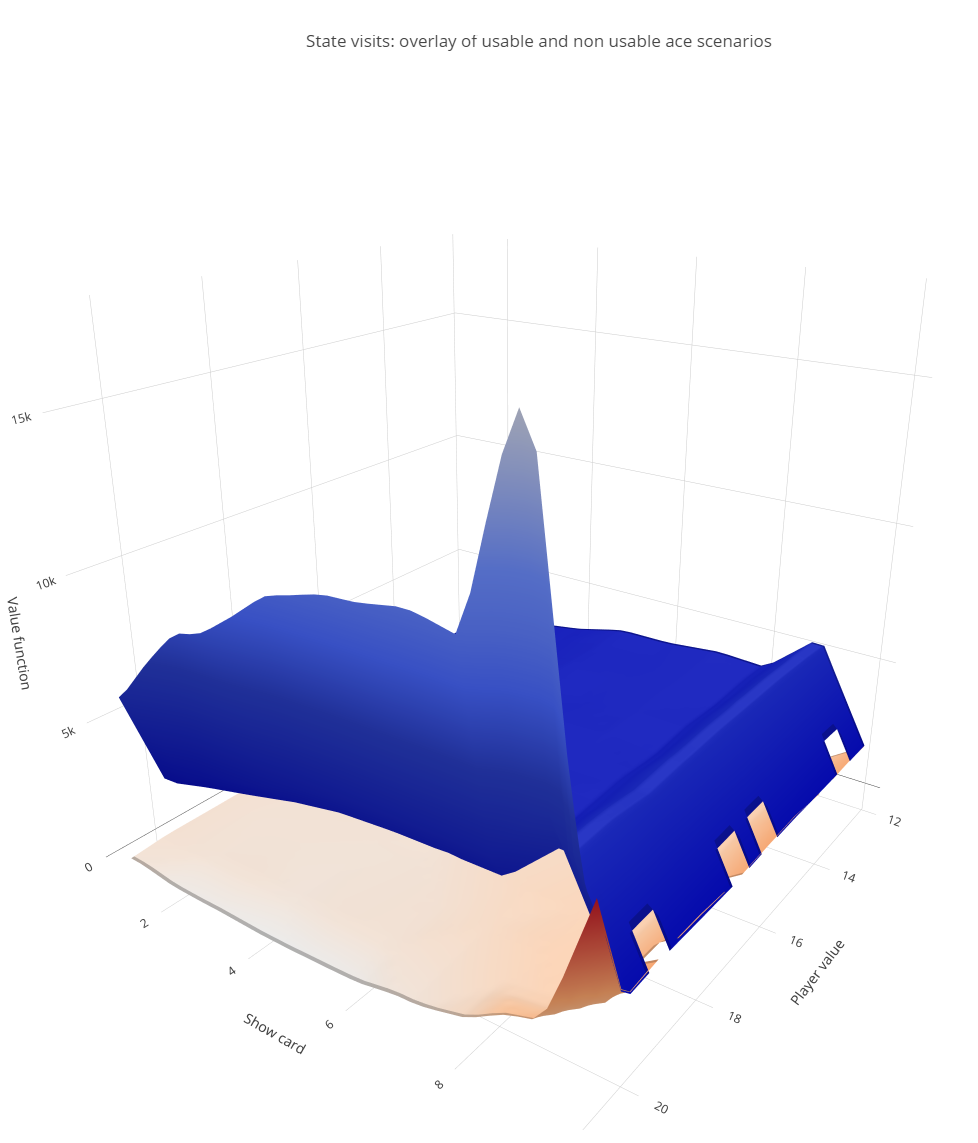
The figure below illustrates the surfaces representing the number of state visits recorded over 500,000 game rounds. It highlights a notable underrepresentation of states in the usable ace scenario compared to the non-usable ace scenario.
Let us now normalize the value function by dividing it by the frequency of visits. The results are shown in the plot below, where the surfaces are now correctly ordered.
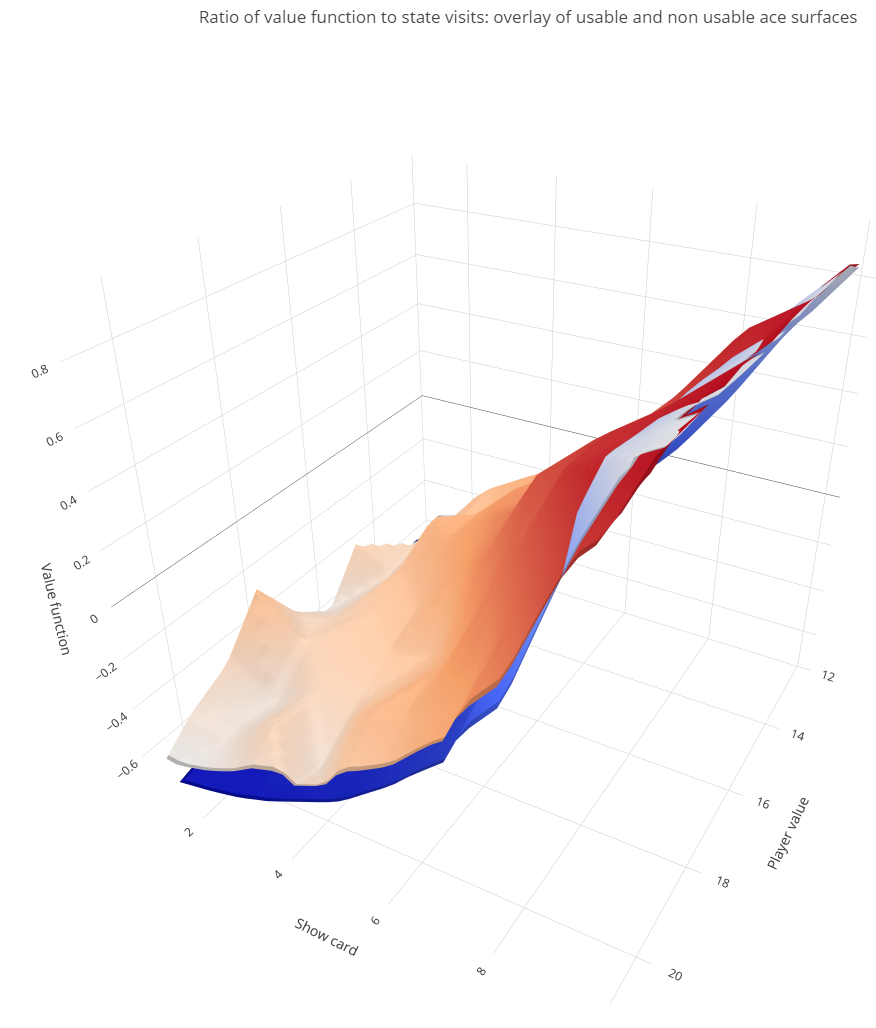
This simple example demonstrates that normalization in policy evaluation is crucial! However, it can be challenging, especially in cases with large state spaces where the distribution of visits might not be accurately estimated. Nevertheless, this factor must be considered when designing algorithms for sampling the state space.
Conclusion
The Monte Carlo approach to policy evaluation in reinforcement learning is an extremely powerful tool. It offers a significant advantage over methods based on the Bellman equation, as the latter requires full prior knowledge of state probabilities. In contrast, the Monte Carlo method approximates these probabilities during the process of sampling. However, this approach has critical implications for value function estimation. To enable accurate inference and decision-making based on the value function, it must be normalized using the probabilities of the respective events or states. In summary, state probabilities must always be incorporated into the reinforcement learning model — either as known values or as estimates derived during the procedure. Failing to normalize the value function after running Monte Carlo sampling can introduce significant decision-making bias, particularly during the policy improvement phase of your reinforcement learning process.
The code replicating the above results is presented below.
Unless otherwise noted, all images are by the author.
References
Sutton, R.S. & Barro, A.G. (1998), Reinforcement Learning, The MIT Press.
Barboianu, C (2022), Understanding Your Game: A Mathematical Advice for Rational and Safe Gambling, INFAROM PhilScience Press.
Why Normalization Is Crucial for Policy Evaluation in Reinforcement Learning was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
from AI in Towards Data Science on Medium https://ift.tt/G3qd16J
via IFTTT




